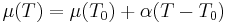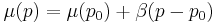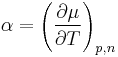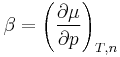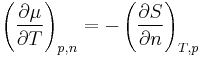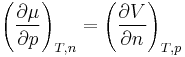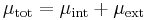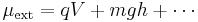Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system.[1] In broadest terms, it is an analogue to electric potential or gravitational potential, utilizing the same idea of force fields as being the cause of things moving, be they charges, masses, or, in this case, chemicals. He defined it as follows:[2]
If to any homogeneous mass in a state of hydrostatic stress we suppose an infinitesimal quantity of any substance to be added, the mass remaining homogeneous and its entropy and volume remaining unchanged, the increase of the energy of the mass divided by the quantity of the substance added is the potential for that substance in the mass considered.
Gibbs later noted also that for the purposes of this definition, any chemical element or combination of elements in given proportions may be considered a substance, whether capable or not of existing by itself as a homogeneous body. Chemical potential is also referred to as partial molar Gibbs energy (see also partial molar property). Chemical potential is measured in units of energy/particle or, equivalently, energy/mole.
The term chemical potential can be used in thermodynamics and physics for any system undergoing change. Chemistry usually restricts the term chemical potential to chemical change or to physical changes that might influence the course of a chemical reaction (phase, concentration, etc.) or to a property such as electron density. In modern statistical physics the chemical potential, divided by the temperature, is the Lagrange multiplier for the average particle constraint, when maximizing the entropy. This is the precise and abstract scientific definition, just like the temperature is defined in terms of the Lagrange multiplier for the average energy constraint.
In some fields (particularly electrochemistry), the term "chemical potential" is used to describe a fundamentally different (but related) concept, namely the "internal chemical potential"; see below for details.
The chemical potential of a system of electrons is also called the Fermi level.[3]
Contents |
Overview
Particles tend to move from higher chemical potential to lower chemical potential. In this way, chemical potential is a generalization of "potentials" in physics such as gravitational potential. When a ball rolls down a hill, it is moving from a higher gravitational potential (higher elevation) to a lower gravitational potential (lower elevation). In the same way, as molecules move, react, dissolve, melt, etc., they will always tend naturally to go from a higher chemical potential to a lower one.
A simple example is a system of dilute molecules diffusing in a homogeneous environment (animation at right). In this system, the molecules tend to move from areas with high concentration to low concentration, until eventually the concentration is the same everywhere. The microscopic explanation for this is based in kinetic theory and the random motion of molecules. However, it is simpler to describe the process in terms of chemical potentials: A molecule has a higher chemical potential in a higher-concentration area, and a lower chemical potential in a low concentration area. As always, the molecules move from higher chemical potential to lower chemical potential.
Another example is a glass of liquid water with ice cubes in it. Above 0°C, an H2O molecule has a lower chemical potential as part of the liquid than as part of an ice cube. The ice melts as the H2O molecules lower their chemical potential. Below 0°C, the ice has a lower chemical potential, so the ice cubes grow. At exactly 0°C, the chemical potential for water and ice are the same; the ice cubes will neither grow nor shrink, and the system is in equilibrium.
In electrochemistry, ions do not always tend to go from higher to lower chemical potential, but they do always go from higher to lower electrochemical potential. The electrochemical potential completely characterizes all of the influences on an ion's motion, while the chemical potential includes everything except the electric force. (See below for more on this terminology.)
History
In his 1873 paper A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces Gibbs introduced the preliminary outline of the principles of his new equation able to predict or estimate the tendencies of various natural processes to ensue when bodies or systems are brought into contact. By studying the interactions of homogeneous substances in contact, i.e. bodies, being in composition part solid, part liquid, and part vapor, and by using a three-dimensional volume–entropy–internal energy graph, Gibbs was able to determine three states of equilibrium, i.e. "necessarily stable", "neutral", and "unstable", and whether or not changes will ensue. In 1876, Gibbs built on this framework by introducing the concept of chemical potential so to take into account chemical reactions and states of bodies that are chemically different from each other. In his own words, to summarize his results in 1873, Gibbs states:
If we wish to express in a single equation the necessary and sufficient condition of thermodynamic equilibrium for a substance when surrounded by a medium of constant pressure P and temperature T, this equation may be written:where δ refers to the variation produced by any variations in the state of the parts of the body, and (when different parts of the body are in different states) in the proportion in which the body is divided between the different states. The condition of stable equilibrium is that the value of the expression in the parenthesis shall be a minimum.
In this description, as used by Gibbs, ε refers to the internal energy of the body, η refers to the entropy of the body, and ν is the volume of the body.
Related terms
The precise meaning of the term chemical potential depends on the context in which it is used.
- When speaking of thermodynamic systems, chemical potential refers to the thermodynamic chemical potential. In this context, the chemical potential is the change in a characteristic thermodynamic state function per change in the number of molecules. Depending on the experimental conditions, the characteristic thermodynamic state function is either: internal energy, enthalpy, Gibbs energy, or Helmholtz energy. This particular usage is most widely used by experimental chemists, physicists, and chemical engineers.
- Theoretical chemists and physicists often use the term chemical potential in reference to the electronic chemical potential, which is related to the functional derivative of the density functional, sometimes called the energy functional, found in Density Functional Theory. This particular usage of the term is widely used in the field of electronic structure theory.
- Physicists sometimes use the term chemical potential in the description of relativistic systems of fundamental particles.
Thermodynamic chemical potential
| Conjugate variables of thermodynamics |
|
|---|---|
| Pressure | Volume |
| (Stress) | (Strain) |
| Temperature | Entropy |
| Chemical potential | Particle number |
The chemical potential of a thermodynamic system is the amount by which the energy of the system would change if an additional particle were introduced, with the entropy and volume held fixed. If a system contains more than one species of particle, there is a separate chemical potential associated with each species, defined as the change in energy when the number of particles of that species is increased by one. The chemical potential is a fundamental parameter in thermodynamics and it is conjugate to the particle number.
The chemical potential is particularly important when studying systems of reacting particles. Consider the simplest case of two species, where a particle of species 1 can transform into a particle of species 2 and vice versa. An example of such a system is a saturated mixture of water liquid (species 1) and water vapor (species 2). If the system is at equilibrium, the chemical potentials of the two species must be equal. Otherwise, a net release of energy in the form of heat would occur (see second law of thermodynamics) when the species of higher potential transforms into the other species, and a net gain of energy (again in the form of heat) would occur for the reverse transformation. In chemical reactions, the equilibrium conditions are generally more complicated because more than two species are involved. In this case, the relation between the chemical potentials at equilibrium is given by the law of mass action.
Since the chemical potential is a thermodynamic quantity, it is defined independently of the microscopic behavior of the system, i.e. the properties of the constituent particles. However, some systems contain important variables that are equivalent to the chemical potential. In Fermi gases and Fermi liquids, the chemical potential at zero temperature is equivalent to the Fermi energy. In electronic systems, the chemical potential is related to an effective electrical potential.
A way to understand the chemical potential is to consider one mole of methane and 2 moles of oxygen. If a flame is brought near this mixture, the following reaction will occur:
and energy (heat) will be released. This energy comes from the difference in chemical potential between CH4 and O2 on one hand (higher potential) and CO2 and H2O on the other hand (lower). The whole energy that will be released will be given by
Similar examples can be found within batteries where chemical energy is converted into electrical energy.
Precise definition
Consider a thermodynamic system containing n constituent species. Its total internal energy U is postulated to be a function of the entropy S, the volume V, and the number of particles of each species N1, ..., Nn
By referring to U as the internal energy, it is emphasized that the energy contributions resulting from the interactions between the system and external objects are excluded. For example, the gravitational potential energy of the system with the Earth are not included in U.
The chemical potential of the i-th species, μi is defined as the partial derivative
where the subscripts simply emphasize that the entropy, volume, and the other particle numbers are to be kept constant.
A similar expression for the chemical potential can be written in terms of partial derivative of the enthalpy (under conditions of constant entropy and pressure).
In real systems, it is usually difficult to hold the entropy fixed, since this involves good thermal insulation. It is therefore more convenient to define the Helmholtz energy A, which is a function of the temperature T, volume, and particle numbers:
In terms of the Helmholtz energy, the chemical potential is
Laboratory experiments are often performed under conditions of constant temperature and pressure. Under these conditions, the chemical potential is the partial derivative of the Gibbs energy with respect to number of particles
Here, the chemical potential has been defined as the energy per molecule. A variant of this definition is to define the chemical potential as the energy per mole.
Electronic chemical potential
The electronic chemical potential is the functional derivative of the density functional with respect to the electron density.
Formally, a functional derivative yields many functions, but is a particular function when evaluated about a reference electron density—just as a derivative yields a function, but is a particular number when evaluated about a reference point. The density functional is written as
where ν(r) is the external potential, e.g., the electrostatic potential of the nuclei and applied fields, and F is the universal functional, which describes the kinetic energy of electrons and electron–electron interactions, e.g. kinetic energy, electron Coulomb repulsion, and the non-classical effects of exchange and correlation. With this general definition of the density functional, the chemical potential is written as
Thus, the electronic chemical potential is the effective electrostatic potential experienced by the electron density.
The ground state electron density is determined by a constrained variational optimization of the electronic energy. The Lagrange multiplier enforcing the density normalization constraint is also called the chemical potential, i.e.,
where  is the number of electrons in the system and
is the number of electrons in the system and  is the Lagrange multiplier enforcing the constraint. When this variational statement is satisfied, the terms within the curly brackets obey the property
is the Lagrange multiplier enforcing the constraint. When this variational statement is satisfied, the terms within the curly brackets obey the property
where the reference density is the density that minimizes the energy. This expression simplifies to
The Lagrange multiplier enforcing the constraint is, by construction, a constant; however, the functional derivative is, in the formal sense, a function. Therefore, when the density minimizes the electronic energy, the chemical potential has the same value at every point in space. The gradient of the chemical potential is an effective electric field. An electric field describes the force per unit charge as a function of space. Therefore, when the density is the ground state density, the electron density is stationary, because the gradient of the chemical potential (which is invariant with respect to position) is zero everywhere; i.e., all forces are balanced. As the density undergoes a change from a non-ground state density to the ground state density, it is said to undergo a process of chemical potential equalization.
The chemical potential of an atom is sometimes said to be the negative of the atom's electronegativity. Likewise, the process of chemical potential equalization is sometimes referred to as the process of electronegativity equalization. This connection comes from the Mulliken definition of electronegativity. By inserting the energetic definitions of the ionization potential and electron affinity into the Mulliken electronegativity, it is possible to show that the Mulliken chemical potential is a finite difference approximation of the electronic energy with respect to the number of electrons., i.e.,
where IP and EA are the ionization potential and electron affinity of the atom, respectively.
The values of the chemical potential
For standard conditions (T = 298.15 K; p = 1 atm) the values of the chemical potential are tabulated, see under "External links". If the chemical potential is known in a certain state (e.g., for standard conditions), then it can be calculated in linear approximation for pressures and temperatures in the vicinity of this state:
and
Here
is the temperature coefficient and
is the pressure coefficient.
With the Maxwell relations
and
it follows that the temperature coefficient is equal to the negative molar entropy and the pressure coefficient is equal to the molar volume.
Fundamental particle chemical potential
In recent years, thermal physics has applied the definition of chemical potential to systems in particle physics and its associated processes. In general, chemical potential measures the tendency of particles to diffuse. This characterization focuses on the chemical potential as a function of spatial location. Particles tend to diffuse from regions of high chemical potential to those of low chemical potential.[4] Being a function of internal energy, chemical potential applies equally to both fermion and boson particles. That is, in theory, any fundamental particle can be assigned a value of chemical potential, depending upon how it changes the internal energy of the system into which it is introduced. The application of chemical potential concepts for systems at absolute zero has significant appeal.
For relativistic systems (i.e., systems in which the rest mass is much smaller than the equivalent thermal energy) the chemical potential is related to symmetries and charges. Each conserved quantity is associated with a chemical potential.
In a gas of photons in equilibrium with massive particles, the number of photons is not conserved, and, so, in this case, the chemical potential is zero. Likewise, for a gas of phonons, there is also no chemical potential. However, if the temperature of such a system were to rise above the threshold for pair production of electrons, then it might be sensible to add a chemical potential for the electrical charge. This would control the electric charge density of the system, and hence the excess of electrons over positrons, but not the number of photons. In the context in which one meets a phonon gas, temperatures high enough to pair produce other particles are seldom relevant. QCD matter is the prime example of a system in which many such chemical potentials appear.
Internal, external, and total chemical potential
When there is a chemical potential difference between two locations, some of it may be due to potentials associated with "external" force fields (Electric potential energy differences, gravitational potential energy differences, etc.), while the rest would be due to "internal" factors (density, temperature, etc.)[5] The true chemical potential, also called total chemical potential, can be split into internal chemical potential and external chemical potential
where
i.e., the external potential is the sum of electric potential, gravitational potential, etc. (q and m are the charge and mass of the species, respectively, V and h are the voltage and height of the container, respectively, and g is the acceleration due to gravity.)
Although the phrase "chemical potential" usually refers to "total chemical potential", this is not universally observed.[5] In some fields, in particular electrochemistry, the term "chemical potential" is instead used to mean internal chemical potential, whereas the term electrochemical potential is used to mean total chemical potential.[6] However, in solid-state physics, precisely the opposite convention is often used in the context of electrons, with "chemical potential" meaning total chemical potential, and "electrochemical potential" meaning internal chemical potential.[7]
See also
- Activity (chemistry)
- Chemical equilibrium
- Electrochemical potential
- Excess chemical potential
- Fugacity
- Partial molar property
- Thermodynamic equilibrium
References
- ^ Physical Chemistry, Peter Atkins and Julio de Paula, W. H Freeman and Company 2010, New York, ISBN 978-1-4292-1812-2
- ^ Human Chemistry(Volume Two), Libb Thims, Libb Thims 2007, ISBN 978-1-4303-1049-5
- ^ Kittel, Charles; Herbert Kroemer (1980-01-15). Thermal Physics (2nd Edition). W. H. Freeman. p. 357. ISBN 978-0716710882. http://books.google.com/?id=c0R79nyOoNMC&pg=PA357.
- ^ Baierlein, Ralph (2003). Thermal Physics. Cambridge University Press. ISBN 0-521-65838-1. OCLC 39633743.
- ^ a b Thermal Physics by Kittel and Kroemer, second edition, page 124.
- ^ See, for example, Electrochemical Methods by Bard and Faulkner, 2nd edition, Section 2.2.4(a),4-5.
- ^ See, for example, Solid State Physics by Ashcroft and Mermin, page 593.
- Baierlein, Ralph (April 2001). "The elusive chemical potential". American Journal of Physics 69 (4): 423–434. Bibcode 2001AmJPh..69..423B. doi:10.1119/1.1336839. http://www.physics.rutgers.edu/ugrad/351/chemical_potential.pdf. Retrieved 2006-11-18.
- Kaplan, T. A. (March 2006). "The Chemical Potential". Journal of Statistical Physics 122 (6): 1237–1260. Bibcode 2006JSP...122.1237K. doi:10.1007/s10955-005-8067-x.
- Job, G.; Herrmann, F. (February 2006). "Chemical potential–a quantity in search of recognition" (PDF). European Journal of Physics 27 (2): 353–371. Bibcode 2006EJPh...27..353J. doi:10.1088/0143-0807/27/2/018. http://www.physikdidaktik.uni-karlsruhe.de/publication/ejp/chem_pot_ejp.pdf.
External links
- Chemical Potential
- Chemical Potentials
- Values of the chemical potential of 1300 substances
- Chemical potential in experiments: Demonstration experiments "dissolution of marble", "ammonia fountain", "carbide lamp" (instructions and videos)
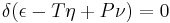
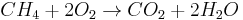
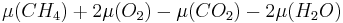
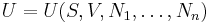
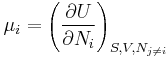
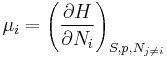
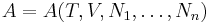
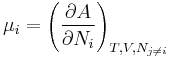
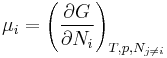
![\mu(\mathbf{r})=\left[ \frac{\delta E[\rho]}{\delta \rho(\mathbf{r})}\right]_{\rho=\rho_{\mathrm{ref}}}](/2012-wikipedia_en_all_nopic_01_2012/I/3580dd3700f4c98fdcfef0d75110ee14.png)
![E[\rho] = \int \rho(\mathbf{r})\nu(\mathbf{r})d^3r %2B F[\rho],](/2012-wikipedia_en_all_nopic_01_2012/I/aa9a3b451a0977acfb6e82118a06f090.png)
![\mu(\mathbf{r}) = \nu(\mathbf{r})%2B\left[\frac{\delta F[\rho]}{\delta\rho(\mathbf{r})}\right]_{\rho=\rho_{\mathrm{ref}}}](/2012-wikipedia_en_all_nopic_01_2012/I/fef2aad6748ecc3edcf37316e62ed9ec.png)
![\delta\left\{E[\rho]-\mu\left(\int\rho(\mathbf{r})d^3r-N\right)\right\}=0](/2012-wikipedia_en_all_nopic_01_2012/I/0fca7e34462ad5e0e22f7b940412835a.png)
![\left[\frac{\delta E[\rho]}{\delta\rho(\mathbf{r})}\right]_{\rho=\rho_{0}} - \mu \left[\frac{\delta N[\rho]}{\delta\rho(\mathbf{r})}\right]_{\rho=\rho_{0}}=0](/2012-wikipedia_en_all_nopic_01_2012/I/3aec43bd395f46674f306e0bf93c6bdb.png)
![\left[\frac{\delta E[\rho]}{\delta\rho(\mathbf{r})}\right]_{\rho=\rho_{0}}=\mu](/2012-wikipedia_en_all_nopic_01_2012/I/ce2c7b195774e6d5edf5ae2eba778bb6.png)
![\mu_{\mathrm{Mulliken}}=-\chi_{\mathrm{Mulliken}}=-\frac{IP%2BEA}{2}=\left[\frac{\delta E[N]}{\delta N}\right]_{N=N_0}](/2012-wikipedia_en_all_nopic_01_2012/I/d0ad966d69609202f1584b44f0f272f5.png)